বিন্যাস (Permutations):

বিন্যাস হল বস্তু গুলিকে একটি নির্দিষ্ট ক্রমে সাজানো। এর জন্য সূত্র:
$$P(n, r) = \frac{n!}{(n - r)!}$$

সমাবেশ (Combinations):

সমাবেশ হল বস্তু গুলিকে বেছে নেওয়া, যেখানে ক্রমের কোনো গুরুত্ব নেই। এর জন্য সূত্র:
$$C(n, r) = \frac{n!}{r!(n - r)!}$$

নির্ণায়ক (Determinants):

নির্ণায়ক একটি ম্যাট্রিক্সের গুণমান। এটি ম্যাট্রিক্সের বিভিন্ন বৈশিষ্ট্য নির্ধারণে সাহায্য করে।

ম্যাট্রিক্স (Matrices):

ম্যাট্রিক্স হল সংখ্যার একটি গাণিতিক কাঠামো যা লিনিয়ার সমীকরণ সমাধান বা ডেটা ব্যবস্থাপনায় ব্যবহৃত হয়।

বিন্যাস (Permutations)

বিন্যাস হল এমন একটি পরিসংখ্যানিক ধারণা যেখানে নির্দিষ্ট সংখ্যা বা বস্তু একত্রিত করার পদ্ধতি নির্ধারণ করা হয়, যেখানে বস্তু গুলির ক্রম (order) গুরুত্বপূর্ণ।

বিন্যাসের সূত্র:
$$P(n, r) = \frac{n!}{(n - r)!}$$
এখানে,

• $n$ হল মোট বস্তু সংখ্যা,
• $r$ হল বাছাইয়ের জন্য বস্তু সংখ্যা,
• $n!$ হল $n$-এর ফ্যাক্টোরিয়াল, অর্থাৎ $n \times (n - 1) \times (n - 2) \times ... \times 1$।

উদাহরণ:

ধরা যাক, একটি বাক্সে 5টি বল রয়েছে (A, B, C, D, E)। এর মধ্যে 3টি বল বেছে নিয়ে তাদের সাজানোর উপায় সংখ্যা কত হবে?

এক্ষেত্রে, $n = 5$ এবং $r = 3$ হবে। তাই,
$$P(5, 3) = \frac{5!}{(5 - 3)!} = \frac{5 \times 4 \times 3!}{2!} = 5 \times 4 \times 3 = 60$$

অর্থাৎ, 5টি বস্তু থেকে 3টি বস্তু বাছাই ও সাজানোর মোট 60টি উপায় রয়েছে।

সমাবেশ (Combinations)

সমাবেশ হলো বস্তু গুলিকে এমনভাবে নির্বাচন করা, যেখানে তাদের মধ্যে কোনো নির্দিষ্ট ক্রম (order) থাকে না। এটি মূলত বস্তু গুলির নির্বাচন নির্ধারণ করে, যেগুলির মধ্যে কোনো ক্রমের গুরুত্ব নেই।

সমাবেশের সূত্র:
$$C(n, r) = \frac{n!}{r!(n - r)!}$$
এখানে,

• $n$ হল মোট বস্তু সংখ্যা,
• $r$ হল বাছাইয়ের জন্য বস্তু সংখ্যা,
• $r!$ এবং $(n - r)!$ হলো যথাক্রমে $r$ এবং $(n - r)$-এর ফ্যাক্টোরিয়াল।

উদাহরণ:

ধরা যাক, একটি বাক্সে 5টি বল রয়েছে (A, B, C, D, E)। এর মধ্যে 3টি বল বেছে নেয়ার উপায় সংখ্যা কত হবে?

এক্ষেত্রে, $n = 5$ এবং $r = 3$ হবে। তাহলে,
$$C(5, 3) = \frac{5!}{3!(5 - 3)!} = \frac{5 \times 4 \times 3!}{3! \times 2!} = \frac{5 \times 4}{2 \times 1} = 10$$

অর্থাৎ, 5টি বস্তু থেকে 3টি বস্তু বাছাই করার 10টি উপায় রয়েছে।

নির্ণায়ক (Determinants)

নির্ণায়ক (Determinant) একটি ম্যাট্রিক্সের গুণমান বা বৈশিষ্ট্য নির্ধারণকারী একটি সংখ্যা। এটি ম্যাট্রিক্সের বিভিন্ন বৈশিষ্ট্য যেমন সমীকরণের সমাধান, বিপরীত ম্যাট্রিক্স (inverse), এবং অন্যান্য গাণিতিক অপারেশন নির্ধারণে ব্যবহৃত হয়।

২x২ ম্যাট্রিক্সের নির্ণায়ক:

ধরা যাক, একটি ২x২ ম্যাট্রিক্স $A$ আছে:
$$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$$
এর নির্ণায়ক হবে:
$$\text{det}(A) = ad - bc$$

৩x৩ ম্যাট্রিক্সের নির্ণায়ক:

ধরা যাক, একটি ৩x৩ ম্যাট্রিক্স $A$ আছে:
$$A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$$
এর নির্ণায়ক হবে:
$$\text{det}(A) = a(ei - fh) - b(di - fg) + c(dh - eg)$$

উদাহরণ:

ধরা যাক, একটি ২x২ ম্যাট্রিক্স $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ দেওয়া আছে।

তাহলে, এর নির্ণায়ক হবে:
$$\text{det}(A) = 1(4) - 2(3) = 4 - 6 = -2$$

নির্ণায়ক একাধিক গাণিতিক প্রয়োগে ব্যবহৃত হয়, যেমন সমীকরণের সমাধান, ইনভার্স ম্যাট্রিক্স খোঁজা, ইত্যাদি।

নির্ণায়ক (Determinant) এর গুণাবলী

নির্ণায়কের কিছু গুরুত্বপূর্ণ গুণাবলী রয়েছে যা ম্যাট্রিক্সের বিভিন্ন গাণিতিক কার্যক্রম এবং বৈশিষ্ট্য বুঝতে সাহায্য করে। এখানে নির্ণায়কের কিছু মৌলিক গুণাবলী এবং সেগুলির প্রমাণ দেওয়া হল:

১. নির্ণায়কের মান পরিবর্তন হয় যদি দুইটি সারি বা কলাম বিনিময় করা হয়।

যদি $A$ একটি $n \times n$ ম্যাট্রিক্স হয় এবং আমরা এর দুটি সারি (বা কলাম) বিনিময় করি, তবে নির্ণায়ক পরিবর্তিত হবে। অর্থাৎ,
$$\text{det}(A') = - \text{det}(A)$$
এখানে, $A'$ হল সেই ম্যাট্রিক্স যেটির দুইটি সারি বা কলাম বিনিময় করা হয়েছে।

প্রমাণ:
ধরা যাক, $A = \begin{bmatrix} a_1 & a_2 & \cdots & a_n \\ b_1 & b_2 & \cdots & b_n \\ \vdots & \vdots & \ddots & \vdots \\ z_1 & z_2 & \cdots & z_n \end{bmatrix}$ একটি $n \times n$ ম্যাট্রিক্স।
যখন দুইটি সারি বিনিময় করা হয়, তখন নির্ণায়কের মানের সাইন পরিবর্তিত হয় (এটি একধরণের গাণিতিক প্রপার্টি)।

২. যদি কোন সারি বা কলামে সমস্ত উপাদান শূন্য থাকে তবে নির্ণায়কের মান শূন্য হবে।

যদি কোনো সারি বা কলাম পুরোপুরি শূন্য থাকে, তবে সেই ম্যাট্রিক্সের নির্ণায়ক শূন্য হবে।
$$\text{det}(A) = 0$$
এখানে, $A$ এমন একটি ম্যাট্রিক্স যার কোনো সারি বা কলাম সম্পূর্ণ শূন্য।

প্রমাণ:
ধরা যাক, $A$ একটি $n \times n$ ম্যাট্রিক্স যার কোনো সারি বা কলাম শূন্য। এতে, নির্ণায়ক হিসাব করার জন্য কোলামের বা সারির উপাদানগুলোর গুণফল শূন্য হবে, ফলে নির্ণায়ক শূন্য হবে।

৩. নির্ণায়ক একটি স্কেলারের সঙ্গে গুণ করলে, গুণফলও স্কেলারের সঙ্গে গুণ হবে।

যদি $A$ একটি $n \times n$ ম্যাট্রিক্স হয় এবং $k$ একটি স্কেলার সংখ্যা হয়, তবে
$$\text{det}(kA) = k^n \cdot \text{det}(A)$$

প্রমাণ:
যখন $A$ ম্যাট্রিক্সের সমস্ত উপাদানকে $k$-এর সাথে গুণ করা হয়, তখন গুণফলে $k$ প্রতিটি সারি বা কলামের জন্য $k$-এর গুণফল হয়, ফলে নির্ণায়কের মান $k^n$ এর গুণফলে পরিণত হয়।

৪. ম্যাট্রিক্সের ট্রান্সপোজের নির্ণায়ক ম্যাট্রিক্সের নির্ণায়ক সমান।

যদি $A$ একটি $n \times n$ ম্যাট্রিক্স হয়, তবে তার ট্রান্সপোজ $A^T$ এর নির্ণায়ক হবে $A$-এর নির্ণায়কের সমান। অর্থাৎ,
$$\text{det}(A^T) = \text{det}(A)$$

প্রমাণ:
ম্যাট্রিক্সের ট্রান্সপোজ করার ফলে সারি এবং কলামের স্থান পরিবর্তিত হয়, কিন্তু নির্ণায়ক পরিবর্তিত হয় না। তাই, $\text{det}(A^T) = \text{det}(A)$ হয়।

৫. যদি ম্যাট্রিক্সের কোনো এক সারি বা কলামে অন্য সারি বা কলামের গুণফল থাকে, তবে নির্ণায়ক শূন্য হবে।

যদি একটি ম্যাট্রিক্সের কোনো সারি বা কলাম অন্য একটি সারি বা কলামের গুণফল হয়, তবে ম্যাট্রিক্সের নির্ণায়ক শূন্য হবে।

প্রমাণ:
ধরা যাক, $A$ একটি $n \times n$ ম্যাট্রিক্স, এবং এর কোনো একটি সারি বা কলাম অন্য একটি সারি বা কলামের গুণফল। এতে, নির্ণায়কের মান শূন্য হবে কারণ ওই সারি বা কলামগুলোর মধ্যে কোনো ভিন্নতা নেই।

উপসংহার

নির্ণায়কের এই গুণাবলী ম্যাট্রিক্সের বিশ্লেষণ এবং গাণিতিক সমীকরণের সমাধানে গুরুত্বপূর্ণ ভূমিকা পালন করে। এগুলো বিভিন্ন গণনাযুক্ত সিদ্ধান্ত এবং গাণিতিক নিয়মাবলী প্রমাণের জন্য ব্যবহার করা হয়।

ম্যাট্রিক্স (Matrices)

ম্যাট্রিক্স হলো একটি গাণিতিক কাঠামো, যা সংখ্যার বা উপাদানের একটি আয়তক্ষেত্রাকার বা স্কয়ার বিন্যাস। এটি লিনিয়ার অ্যালজেব্রা, পরিসংখ্যান, গাণিতিক মডেলিং, এবং অন্যান্য গাণিতিক এবং প্রকৌশল সমস্যা সমাধানে ব্যবহৃত হয়।

ম্যাট্রিক্সের সংজ্ঞা

একটি ম্যাট্রিক্স একটি $m \times n$ আয়তক্ষেত্রাকার গাণিতিক কাঠামো, যার মধ্যে $m$ সারি (rows) এবং $n$ কলাম (columns) থাকে। প্রতিটি উপাদান একটি নির্দিষ্ট সারি ও কলামের交মিলনে থাকে।

এটি সাধারণত এর উপাদানগুলি $a_{ij}$ দিয়ে প্রকাশ করা হয়, যেখানে $i$ সারির সূচক এবং $j$ কলামের সূচক।

যেমন একটি ৩x৩ ম্যাট্রিক্স $A$ হবে:
$$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \end{bmatrix}$$

এখানে, $a_{ij}$ ম্যাট্রিক্সের উপাদান, যেখানে $i$ সারি এবং $j$ কলামের সূচক।

ম্যাট্রিক্সের প্রধান প্রকার

1. স্কয়ার ম্যাট্রিক্স (Square Matrix):
   একটি ম্যাট্রিক্স যেখানে সারি এবং কলামের সংখ্যা সমান, তাকে স্কয়ার ম্যাট্রিক্স বলে। উদাহরণস্বরূপ, $3 \times 3$ ম্যাট্রিক্স।
2. রেকট্যাঙ্গুলার ম্যাট্রিক্স (Rectangular Matrix):
   একটি ম্যাট্রিক্স যেখানে সারি এবং কলামের সংখ্যা আলাদা থাকে, তাকে রেকট্যাঙ্গুলার ম্যাট্রিক্স বলে।
3. শূন্য ম্যাট্রিক্স (Zero Matrix):
   একটি ম্যাট্রিক্স যেখানে সমস্ত উপাদানই শূন্য হয়, তাকে শূন্য ম্যাট্রিক্স বলে। উদাহরণ:
   $$A = \begin{bmatrix} 0 & 0 & 0 \ 0 & 0 & 0 \ 0 & 0 & 0 \end{bmatrix}$$
4. এম্পিউটিটি ম্যাট্রিক্স (Identity Matrix):
   একটি স্কয়ার ম্যাট্রিক্স, যেখানে মূল রেখায় (diagonal) সমস্ত উপাদান ১ থাকে এবং বাকি সব উপাদান শূন্য থাকে। উদাহরণ:
   $$I = \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix}$$
5. ট্রান্সপোজ ম্যাট্রিক্স (Transpose Matrix):
   একটি ম্যাট্রিক্সের সারি এবং কলামের স্থান পরিবর্তন করলে তাকে তার ট্রান্সপোজ বলা হয়। একটি ম্যাট্রিক্স $A$-এর ট্রান্সপোজ $A^T$ হবে, যেখানে:
   $$A^T = \text{Transpose of } A$$
6. বিপরীত ম্যাট্রিক্স (Inverse Matrix):
   একটি স্কয়ার ম্যাট্রিক্স $A$ এর বিপরীত $A^{-1}$ তখনই অস্তিত্ব হয় যখন $A$ একটি ইনভার্সেবল ম্যাট্রিক্স হয়, অর্থাৎ $A \times A^{-1} = I$।

ম্যাট্রিক্সের কিছু সাধারণ অপারেশন

1. ম্যাট্রিক্স যোগফল (Matrix Addition):
   দুটি ম্যাট্রিক্স যোগ করার জন্য তাদের আকার সমান হতে হবে। দুটি ম্যাট্রিক্সের উপাদানগুলোর যোগফল করতে হয়। উদাহরণ:
   $$A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \ 7 & 8 \end{bmatrix}$$
   $$A + B = \begin{bmatrix} 1+5 & 2+6 \ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \ 10 & 12 \end{bmatrix}$$
2. ম্যাট্রিক্স গুণফল (Matrix Multiplication):
   দুটি ম্যাট্রিক্স গুণ করতে হলে প্রথম ম্যাট্রিক্সের কলামের সংখ্যা দ্বিতীয় ম্যাট্রিক্সের সারির সমান হতে হবে। উদাহরণ:
   $$A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \ 7 & 8 \end{bmatrix}$$
   $$A \times B = \begin{bmatrix} (1 \times 5 + 2 \times 7) & (1 \times 6 + 2 \times 8) \ (3 \times 5 + 4 \times 7) & (3 \times 6 + 4 \times 8) \end{bmatrix} = \begin{bmatrix} 19 & 22 \ 43 & 50 \end{bmatrix}$$
3. ম্যাট্রিক্স স্কেলার গুণ (Scalar Multiplication):
   একটি ম্যাট্রিক্সকে একটি স্কেলার সংখ্যার সাথে গুণ করলে, তার সমস্ত উপাদান সেই স্কেলার সংখ্যার সাথে গুণ হয়। উদাহরণ:
   $$A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \quad k = 2$$
   $$k \times A = \begin{bmatrix} 2 \times 1 & 2 \times 2 \ 2 \times 3 & 2 \times 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \ 6 & 8 \end{bmatrix}$$

উপসংহার

ম্যাট্রিক্স গাণিতিক সমস্যা সমাধানে একটি অত্যন্ত গুরুত্বপূর্ণ উপাদান। এটি লিনিয়ার সমীকরণ সমাধান, গাণিতিক মডেলিং, পরিসংখ্যান, ডিজাইন অ্যানালিসিস, এবং অন্যান্য শাখায় ব্যাপকভাবে ব্যবহৃত হয়।

ম্যাট্রিক্সের বিভিন্ন সূত্র ও তার প্রমাণ

ম্যাট্রিক্সের অনেক মৌলিক গাণিতিক সূত্র রয়েছে, যা ম্যাট্রিক্সের অপারেশন ও বিভিন্ন গাণিতিক প্রয়োগে ব্যবহৃত হয়। এখানে কিছু গুরুত্বপূর্ণ সূত্র এবং তার প্রমাণ দেওয়া হলো:

১. ম্যাট্রিক্স যোগফলের কমিউটেটিভিটি (Commutativity of Matrix Addition)

সূত্র:
$$A + B = B + A$$
এখানে, $A$ এবং $B$ একই আকারের দুটি ম্যাট্রিক্স।

প্রমাণ:
যেহেতু ম্যাট্রিক্সের যোগফলে প্রতিটি উপাদান শুধুমাত্র ঐ দুইটি ম্যাট্রিক্সের সংশ্লিষ্ট উপাদানের যোগফল হয়, তাই,
$$A + B = \begin{bmatrix} a_{ij} + b_{ij} \end{bmatrix}, \quad B + A = \begin{bmatrix} b_{ij} + a_{ij} \end{bmatrix}$$
এবং যেহেতু $a_{ij} + b_{ij} = b_{ij} + a_{ij}$, এটি কমিউটেটিভ প্রপার্টি।

২. ম্যাট্রিক্স গুণফলের অ্যাসোসিয়েটিভিটি (Associativity of Matrix Multiplication)

সূত্র:
$$A(BC) = (AB)C$$
এখানে, $A$, $B$, এবং $C$ হল ম্যাট্রিক্স, এবং $AB$, $BC$ তাদের গুণফল।

প্রমাণ:
ম্যাট্রিক্স গুণফলে প্রতিটি উপাদান কলাম এবং সারির গুণফল হয়। এই গুণফল কম্পিউট করার সময় অ্যাসোসিয়েটিভ প্রপার্টি ঠিকভাবে কাজ করে, কারণ গুণফলে প্রতিটি উপাদান পর্যায়ক্রমে গুণ হয়। তাই $A(BC) = (AB)C$ হবে।

৩. ম্যাট্রিক্সের স্কেলারের সঙ্গে গুণফল (Scalar Multiplication of Matrices)

সূত্র:
$$k(A + B) = kA + kB$$
এখানে, $A$ এবং $B$ হল ম্যাট্রিক্স এবং $k$ একটি স্কেলার সংখ্যা।

প্রমাণ:
ম্যাট্রিক্স $A$ এবং $B$-এর উপাদানগুলো যখন স্কেলার $k$-এর সাথে গুণ করা হয়, তখন এটি হবে:
$$k(A + B) = k \begin{bmatrix} a_{ij} + b_{ij} \end{bmatrix} = \begin{bmatrix} k(a_{ij} + b_{ij}) \end{bmatrix}$$
এবং,
$$kA + kB = \begin{bmatrix} k a_{ij} \end{bmatrix} + \begin{bmatrix} k b_{ij} \end{bmatrix} = \begin{bmatrix} k(a_{ij} + b_{ij}) \end{bmatrix}$$
এটা সমান হবে। তাই, $k(A + B) = kA + kB$ প্রমাণিত হলো।

৪. ম্যাট্রিক্স গুণফল এবং স্কেলার গুণ (Matrix Multiplication and Scalar Multiplication)

সূত্র:
$$k(AB) = (kA)B = A(kB)$$
এখানে, $A$, $B$ ম্যাট্রিক্স এবং $k$ একটি স্কেলার সংখ্যা।

প্রমাণ:
$k$ স্কেলার সংখ্যাটি গুণফলের উপর বিতরণযোগ্য। অর্থাৎ, $k$-এর সাথে গুণফলে প্রতিটি উপাদানকে $k$-এর গুণফলে গুণ করা হয়। তাই,
$$k(AB) = \begin{bmatrix} k \times (a_{ij} \times b_{ij}) \end{bmatrix}$$
এবং,
$$(kA)B = \begin{bmatrix} (k \times a_{ij}) \times b_{ij} \end{bmatrix}, \quad A(kB) = \begin{bmatrix} a_{ij} \times (k \times b_{ij}) \end{bmatrix}$$
তাহলে, $k(AB) = (kA)B = A(kB)$ প্রমাণিত হলো।

৫. ম্যাট্রিক্সের ট্রান্সপোজের গুণফল (Transpose of a Matrix)

সূত্র:
$$(AB)^T = B^T A^T$$
এখানে, $A$ এবং $B$ ম্যাট্রিক্স।

প্রমাণ:
$AB$-এর ট্রান্সপোজ হবে:
\[
(AB)^T = \begin{bmatrix} (AB){ij} \end{bmatrix}^T = \begin{bmatrix} (AB){ji} \end{bmatrix}
\]
এবং,
$$B^T A^T = \begin{bmatrix} B_{ij} \end{bmatrix}^T \begin{bmatrix} A_{ij} \end{bmatrix}^T = \begin{bmatrix} B_{ji} A_{ji} \end{bmatrix}$$
তাহলে, $(AB)^T = B^T A^T$ প্রমাণিত হলো।

৬. ম্যাট্রিক্সের ইনভার্সের গুণফল (Inverse of Matrix)

সূত্র:
$$A^{-1}A = I$$
এখানে, $A^{-1}$ হল $A$-এর ইনভার্স, এবং $I$ হল ঐ ম্যাট্রিক্সের আইডেন্টিটি ম্যাট্রিক্স।

প্রমাণ:
যেহেতু $A^{-1}$ হল $A$-এর ইনভার্স, এবং ইনভার্সের সংজ্ঞা অনুযায়ী,
$$A^{-1}A = I$$
এটি গাণিতিকভাবে সঠিক।

৭. ডিটারমিন্যান্টের গুণফল (Determinant of a Matrix Product)

সূত্র:
$$\text{det}(AB) = \text{det}(A) \times \text{det}(B)$$
এখানে, $A$ এবং $B$ ম্যাট্রিক্স।

প্রমাণ:
ডিটারমিন্যান্টের গুণফলে এটি প্রমাণ করা যায় যে, যখন দুটি ম্যাট্রিক্সের গুণফল হবে, তাদের ডিটারমিন্যান্টের গুণফল হবে। এটি একটি সাধারণ গাণিতিক তত্ত্ব যা ম্যাট্রিক্সের উপাদানের উপর ভিত্তি করে কাজ করে।

এই গুণাবলীর সাহায্যে ম্যাট্রিক্সের বিভিন্ন গাণিতিক সমীকরণ এবং প্রয়োগ করা যায়। এগুলো লিনিয়ার অ্যালজেব্রা, সিস্টেম অফ লিনিয়ার ইকুয়েশন, এবং পরিসংখ্যান বা অন্যান্য গাণিতিক সমস্যা সমাধানে অত্যন্ত গুরুত্বপূর্ণ।

প্রাক্কলন (Estimation) এইচএসসি পরিসংখ্যানে: বিস্তারিত আলোচনা

প্রাক্কলন পরিসংখ্যানের একটি গুরুত্বপূর্ণ অধ্যায় যা আমাদের অনুমান করতে সাহায্য করে যে, কোনো জনসংখ্যার নির্দিষ্ট বৈশিষ্ট্য কেমন হতে পারে। এটি বিভিন্ন বাস্তব সমস্যার সমাধান এবং সিদ্ধান্ত গ্রহণে গুরুত্বপূর্ণ ভূমিকা পালন করে।

প্রাক্কলনের সংজ্ঞা

প্রাক্কলন হলো একটি পদ্ধতি যার মাধ্যমে একটি ছোট নমুনার সাহায্যে জনসংখ্যার একটি বৈশিষ্ট্যের মান নির্ধারণ করা হয়।

• উদাহরণস্বরূপ, একটি এলাকার মানুষের গড় আয়ের প্রাক্কলন করতে কয়েকজন মানুষের আয় নিয়ে গড় হিসাব করা হয়।

প্রাক্কলনের প্রকারভেদ

১. বিন্দু প্রাক্কলন (Point Estimation)

এটি এমন একটি পদ্ধতি যেখানে জনসংখ্যার নির্দিষ্ট বৈশিষ্ট্যের একটি একক মান নির্ধারণ করা হয়।

• উদাহরণ: একটি এলাকার মানুষের গড় উচ্চতা হলো ৫ ফুট ৬ ইঞ্চি।

গুণাবলি:

• সরাসরি ফলাফল প্রদান করে।
• সাধারণত গড়, মধ্যমা, এবং মোড ব্যবহার করা হয়।

২. বিস্তার প্রাক্কলন (Interval Estimation)

এটি এমন একটি পদ্ধতি যেখানে নির্দিষ্ট সীমার মধ্যে জনসংখ্যার বৈশিষ্ট্যের মান নির্ধারণ করা হয়।

• উদাহরণ: একটি এলাকার গড় আয়ের প্রাক্কলিত সীমা হলো $২০,০০০ থেকে $২৫,০০০।

গুণাবলি:

• এটি আরও নির্ভুল এবং সঠিক ফলাফল প্রদান করে।
• "বিশ্বাসযোগ্যতার স্তর" (Confidence Level) ব্যবহৃত হয়, যেমন ৯৫% বা ৯৯%।

প্রাক্কলনের উপাদান

১. জনসংখ্যা (Population):

যে সমগ্র সেট থেকে নমুনা নেওয়া হয়।

• উদাহরণ: একটি দেশের সকল মানুষের গড় আয়।

২. নমুনা (Sample):

জনসংখ্যার একটি ছোট অংশ যা পরিসংখ্যান বিশ্লেষণে ব্যবহৃত হয়।

• উদাহরণ: ১০০ জনের গড় আয় দিয়ে দেশের গড় আয়ের প্রাক্কলন।

৩. পরিসংখ্যান (Statistic):

নমুনার উপর ভিত্তি করে গাণিতিক হিসাব।

• উদাহরণ: নমুনা গড়।

৪. প্যারামিটার (Parameter):

জনসংখ্যার বৈশিষ্ট্যের প্রকৃত মান।

• উদাহরণ: জনসংখ্যার গড়।

বিশ্বাসযোগ্যতার স্তর (Confidence Level)

প্রাক্কলনের নির্ভুলতা নির্ধারণে ব্যবহার করা হয়।

• ৯৫% বিশ্বাসযোগ্যতার স্তর:
  ৯৫% নিশ্চিত যে প্রাক্কলিত সীমার মধ্যে জনসংখ্যার মান থাকবে।
• ৯৯% বিশ্বাসযোগ্যতার স্তর:
  আরও বেশি নির্ভুল প্রাক্কলন, তবে বিস্তারও বেশি।

প্রাক্কলন পদ্ধতি

গাণিতিক পদ্ধতি:

১. গড়ের ব্যবহার (Mean):
নমুনার গড় ব্যবহার করে প্রাক্কলন করা হয়।
$\bar{x} = \frac{\Sigma x}{n}$

২. মধ্যমার ব্যবহার (Median):
নমুনার মধ্যবর্তী মান ব্যবহার করা হয়।
উদাহরণ: নমুনা আয় $[২০, ২২, ২৪, ২৬, ২৮]$, এখানে মধ্যমা $২৪$।

আনুমানিক পদ্ধতি:

১. পূর্ববর্তী তথ্যের ব্যবহার।
২. পূর্ব অভিজ্ঞতার উপর ভিত্তি করে সিদ্ধান্ত।

• উদাহরণ: কোনো বিশেষ অঞ্চলের গড় আয়ের পরিবর্তনের হার দিয়ে ভবিষ্যৎ আয়ের প্রাক্কলন।

বাস্তব জীবনে প্রাক্কলনের ব্যবহার

অর্থনীতি:

দেশের জিডিপি, জনসংখ্যার প্রবৃদ্ধি বা গড় আয় প্রাক্কলনে ব্যবহৃত হয়।

ব্যবসায়:

নতুন পণ্যের চাহিদা নির্ধারণ, উৎপাদন পরিকল্পনা ইত্যাদিতে সাহায্য করে।

গবেষণা:

বিজ্ঞান ও প্রযুক্তিতে পরীক্ষার ফলাফলের প্রাক্কলন।

উদাহরণসমূহ

১. গড় আয়:

নমুনা আয় $২০,০০০, $২৫,০০০ এবং $২২,০০০।

২. বৃষ্টিপাতের সীমা:

নমুনার উপর ভিত্তি করে প্রাক্কলিত সীমা:
$১৫০ \text{ মিমি } - ২০০ \text{ মিমি}$।

সারসংক্ষেপ

প্রাক্কলন হলো একটি কার্যকর পদ্ধতি যা পরিসংখ্যানের মাধ্যমে ভবিষ্যৎ বা অজানা মান সম্পর্কে ধারণা দেয়। এটি অর্থনীতি, ব্যবসা, গবেষণা এবং আরও অনেক ক্ষেত্রে সিদ্ধান্ত গ্রহণে সাহায্য করে।

প্রাক্কলন পদ্ধতি (Estimation Methods)

পরিসংখ্যানে প্রাক্কলনের মাধ্যমে নমুনা থেকে জনসংখ্যার বৈশিষ্ট্য অনুমান করা হয়। প্রাক্কলনের পদ্ধতিগুলো মূলত দুই ধরনের: গাণিতিক পদ্ধতি এবং আনুমানিক পদ্ধতি।

গাণিতিক পদ্ধতি (Statistical Methods)

গাণিতিক পদ্ধতিতে প্রাক্কলন করার জন্য নমুনা থেকে গণিত ও পরিসংখ্যানের বিভিন্ন সূত্র ব্যবহার করা হয়। এগুলোর মধ্যে উল্লেখযোগ্য হলো:

গড়ের ব্যবহার (Mean)

• নমুনার গড় ব্যবহার করে প্রাক্কলন করা হয়।
• সূত্র:
  $$\bar{x} = \frac{\Sigma x}{n}$$
  এখানে,
  $\bar{x}$ = নমুনার গড়
  $\Sigma x$ = নমুনার মানগুলোর যোগফল
  $n$ = নমুনার সংখ্যা

উদাহরণ:
যদি কোনো এলাকার নমুনা আয়ের মান হয় $২০,০০০, $২৫,০০০ এবং $২২,০০০, তবে গড়:
$$\bar{x} = \frac{২০০০০ + ২৫০০০ + ২২০০০}{৩} = ২২,৩৩৩$$

মধ্যমার ব্যবহার (Median)

• নমুনার মধ্যবর্তী মান ব্যবহার করে জনসংখ্যার বৈশিষ্ট্য প্রাক্কলন করা হয়।
• এটি এমন পরিস্থিতিতে কার্যকর যেখানে গড় অতিরিক্ত বড় বা ছোট মান দ্বারা প্রভাবিত হয়।

উদাহরণ:
নমুনা আয়: $১৮,০০০, $২০,০০০, $২২,০০০, $২৪,০০০, এবং $২৬,০০০।
মধ্যমা: $২২,০০০ (মধ্যবর্তী মান)।

মোডের ব্যবহার (Mode)

• নমুনায় সবচেয়ে ঘন ঘন উপস্থিত মান ব্যবহার করা হয়।
• এটি প্রাক্কলনের জন্য সহায়ক যেখানে একটি নির্দিষ্ট বৈশিষ্ট্যের সবচেয়ে সাধারণ মান জানতে হবে।

উদাহরণ:
নমুনা: $১৫,০০০, $২০,০০০, $২০,০০০, $২৫,০০০।
মোড: $২০,০০০ (সবচেয়ে ঘন ঘন উপস্থিত)।

বিস্তার প্রাক্কলন (Interval Estimation)

• গাণিতিক পদ্ধতিতে নির্দিষ্ট সীমার মধ্যে প্রাক্কলন করা হয়।
• বিশ্বাসযোগ্যতার স্তর (Confidence Level) নির্ধারণ করা হয়, যেমন ৯৫% বা ৯৯%।

সূত্র:
$$\bar{x} \pm Z \cdot \frac{s}{\sqrt{n}}$$
যেখানে,
$\bar{x}$ = নমুনার গড়
$Z$ = নির্দিষ্ট বিশ্বাসযোগ্যতার স্তরের জন্য Z-স্কোর
$s$ = নমুনার মান বিচ্যুতি
$n$ = নমুনার সংখ্যা

আনুমানিক পদ্ধতি (Heuristic Methods)

আনুমানিক পদ্ধতি পূর্ব অভিজ্ঞতা এবং বাস্তবতার উপর ভিত্তি করে করা হয়।

১. পূর্ববর্তী তথ্যের ব্যবহার:

• আগে সংগৃহীত তথ্য বা পূর্ববর্তী পরীক্ষার ফলাফল থেকে প্রাক্কলন করা হয়।
• উদাহরণ: একটি এলাকার গত ৫ বছরের গড় বৃষ্টিপাত থেকে এ বছরের বৃষ্টিপাতের সম্ভাবনা নির্ধারণ।

২. অভিজ্ঞতার ব্যবহার:

• গবেষক বা বিশেষজ্ঞের অভিজ্ঞতার ভিত্তিতে প্রাক্কলন।
• উদাহরণ: কোনো নির্দিষ্ট অঞ্চলে চাষাবাদের সম্ভাব্য ফলন অনুমান করা।

৩. পূর্বাভাস পদ্ধতি (Forecasting Techniques):

• ঐতিহাসিক প্রবণতা বিশ্লেষণ করে ভবিষ্যৎ অনুমান।
• উদাহরণ: একটি কোম্পানির বিক্রয়ের প্রবণতা দেখে ভবিষ্যতের বিক্রয় পরিমাণ প্রাক্কলন।

উদাহরণ: প্রাক্কলন পদ্ধতি প্রয়োগ

উদাহরণ ১: গড়ের পদ্ধতি

নমুনা: $১০,০০০, $১২,০০০, $১৪,০০০।
গড়:

উদাহরণ ২: বিস্তার প্রাক্কলন

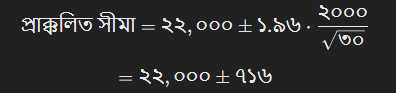
নমুনার গড়: $২২,০০০
বিশ্বাসযোগ্যতার স্তর: ৯৫%
$Z = ১.৯৬, s = ২,০০০, n = ৩০$

সীমা: $২১,২৮৪ থেকে $২২,৭১৬।

সারসংক্ষেপ

প্রাক্কলন পদ্ধতিতে গাণিতিক এবং আনুমানিক উভয় পদ্ধতি ব্যবহার করা হয়। গাণিতিক পদ্ধতি অধিক নির্ভুল এবং পরিসংখ্যানের উপর ভিত্তি করে ফলাফল প্রদান করে, যেখানে আনুমানিক পদ্ধতি বাস্তব পরিস্থিতি ও অভিজ্ঞতার উপর নির্ভর করে।

প্রাক্কলনের ধর্ম (Properties of Estimation)

প্রাক্কলনের ধর্মগুলো নির্ধারণ করে যে একটি প্রাক্কলন কতটা কার্যকর এবং সঠিক। কার্যকর প্রাক্কলন পদ্ধতিকে চিহ্নিত করতে নিম্নলিখিত ধর্মগুলো বিবেচনা করা হয়:

১. পক্ষপাতহীনতা (Unbiasedness)

• একটি প্রাক্কলন পক্ষপাতহীন হতে হবে, অর্থাৎ প্রাক্কলকের (estimator) গড় মান জনসংখ্যার প্রকৃত প্যারামিটারের সমান হতে হবে।
• সূত্র:
  $$E(\hat{\theta}) = \theta$$
  এখানে,
  $\hat{\theta}$ = প্রাক্কলকের গড় মান
  $\theta$ = জনসংখ্যার প্রকৃত প্যারামিটার

উদাহরণ:
যদি কোনো এলাকার গড় আয়ের প্রকৃত মান $২০,০০০ এবং প্রাক্কলিত গড় বারবার $২০,০০০ প্রদান করে, তবে এটি পক্ষপাতহীন।

২. সামঞ্জস্যতা (Consistency)

• একটি প্রাক্কলন সামঞ্জস্যপূর্ণ হলে, নমুনার আকার বৃদ্ধি পেলে প্রাক্কলন জনসংখ্যার প্রকৃত প্যারামিটারের নিকটবর্তী হবে।
• অর্থাৎ, $n \to \infty$ হলে $\hat{\theta} \to \theta$।

উদাহরণ:
১০০ জনের নমুনার ভিত্তিতে গড় আয় $১৯,৮০০ এবং ১০০০ জনের নমুনার ভিত্তিতে গড় আয় $১৯,৯৫০, এটি সামঞ্জস্যপূর্ণ।

৩. দক্ষতা (Efficiency)

• প্রাক্কলকের বৈচিত্র্য (variance) যত কম, সেটি তত বেশি দক্ষ।
• কম বৈচিত্র্য মানে প্রাক্কলন পদ্ধতি নির্ভুল।
• সূত্র:
  $$Var(\hat{\theta})$$
  এখানে, $\hat{\theta}$-এর বৈচিত্র্য যত কম হবে, এটি তত বেশি কার্যকর হবে।

উদাহরণ:
দুইটি প্রাক্কলকের মধ্যে একটির বৈচিত্র্য ১০ এবং অপরটির বৈচিত্র্য ১৫। প্রথমটি বেশি কার্যকর।

৪. যথার্থতা (Sufficiency)

• যথার্থ প্রাক্কলক এমন একটি প্রাক্কলন পদ্ধতি যা প্রাসঙ্গিক তথ্য ব্যবহার করে।
• যথার্থ প্রাক্কলক সব প্রয়োজনীয় তথ্য ধারণ করে এবং কোন তথ্য বাদ দেয় না।

উদাহরণ:
নমুনার প্রতিটি মান ব্যবহার করে গড় নির্ধারণ যথার্থ প্রাক্কলন।

৫. সহমিতি (Robustness)

• প্রাক্কলক সহমিতি তখনই বলে যখন এটি বিভিন্ন ধরনের তথ্য বা শর্তেও কার্যকর থাকে।
• উদাহরণ: প্রাক্কলকের উপর অস্বাভাবিক মান (outlier) প্রভাব ফেলবে না।

প্রাক্কলনের ধর্মগুলোর প্রমাণ

প্রাক্কলনের ধর্মগুলো প্রমাণ করার জন্য গাণিতিক সূত্র এবং পরিসংখ্যানের বিভিন্ন নিয়ম ব্যবহার করা হয়। এখানে কয়েকটি গুরুত্বপূর্ণ প্রমাণ উল্লেখ করা হলো:

১. পক্ষপাতহীনতার প্রমাণ

ধরা যাক, $\hat{\theta}$ একটি প্রাক্কলক এবং জনসংখ্যার প্যারামিটার $\theta$।
পক্ষপাতহীনতার জন্য,
$$E(\hat{\theta}) = \theta$$

উদাহরণ: গড়ের ক্ষেত্রে,
$$\hat{\mu} = \frac{\Sigma x}{n}$$
এবং,
$$E(\hat{\mu}) = \mu$$
অতএব, গড় একটি পক্ষপাতহীন প্রাক্কলক।

২. সামঞ্জস্যতার প্রমাণ

ধরা যাক, \( \hat{\theta}n \) একটি প্রাক্কলক। সামঞ্জস্যতার জন্য,
\[
\lim{n \to \infty} P(|\hat{\theta}_n - \theta| < \epsilon) = 1
\]
অর্থাৎ, $n$-এর মান বাড়ালে প্রাক্কলক $\theta$-এর কাছাকাছি পৌঁছাবে।

৩. দক্ষতার প্রমাণ

ধরা যাক, $\hat{\theta}_1$ এবং $\hat{\theta}_2$ দুইটি প্রাক্কলক। যদি,
$$Var(\hat{\theta}_1) < Var(\hat{\theta}_2)$$
তাহলে, $\hat{\theta}_1$ বেশি কার্যকর।

উদাহরণ:
গড়ের প্রাক্কলনের জন্য,
$$Var(\bar{x}) = \frac{\sigma^2}{n}$$
এটি দেখায় যে নমুনার আকার বৃদ্ধির সঙ্গে গড়ের বৈচিত্র্য কমে যায়।

৪. যথার্থতার প্রমাণ

ধরা যাক, $\hat{\theta}$ একটি যথার্থ প্রাক্কলক। এটি জনসংখ্যার সমস্ত প্রাসঙ্গিক তথ্য ধারণ করবে।
পরীক্ষার জন্য, যথার্থ প্রাক্কলক সর্বাধিক সম্ভাব্যতা (maximum likelihood) পদ্ধতি দিয়ে যাচাই করা হয়।

সারসংক্ষেপ

প্রাক্কলনের ধর্মগুলো কার্যকর এবং নির্ভুল প্রাক্কলন পদ্ধতি নির্ধারণে সাহায্য করে। পক্ষপাতহীনতা, সামঞ্জস্যতা, দক্ষতা, যথার্থতা এবং সহমিতি একটি প্রাক্কলন পদ্ধতির সঠিকতা প্রমাণ করে। এগুলোর গাণিতিক ভিত্তি এবং ব্যবহারিক প্রয়োগ নিশ্চিত করে যে প্রাক্কলন বাস্তব জীবনের সমস্যাগুলো সমাধানে কার্যকর।

অন্তর প্রাক্কলন (Interval Estimation)

অন্তর প্রাক্কলন হলো পরিসংখ্যানের এমন একটি পদ্ধতি যেখানে জনসংখ্যার কোনো নির্দিষ্ট বৈশিষ্ট্যের মান একটি সীমার (interval) মধ্যে নির্ধারণ করা হয়। এটি বিন্দু প্রাক্কলনের তুলনায় বেশি নির্ভুল এবং সঠিক কারণ এটি একটি সম্ভাব্য সীমার মধ্যে ফলাফল প্রদান করে।

অন্তর প্রাক্কলনের ধারণা

• অন্তর প্রাক্কলনের মাধ্যমে প্রাক্কলিত মান একটি নিম্ন সীমা এবং উচ্চ সীমার মধ্যে থাকে।
• এই প্রক্রিয়ায় "বিশ্বাসযোগ্যতার স্তর" (Confidence Level) উল্লেখ করা হয়, যা নির্ধারণ করে যে জনসংখ্যার প্রকৃত মান এই সীমার মধ্যে কত শতাংশ নিশ্চিতভাবে থাকবে।

অন্তর প্রাক্কলনের উপাদান

১. নিম্ন সীমা (Lower Bound):

সীমার নিচের মান, যা একটি প্রাক্কলনের সর্বনিম্ন সম্ভাব্য মান।

২. উচ্চ সীমা (Upper Bound):

সীমার উপরের মান, যা একটি প্রাক্কলনের সর্বোচ্চ সম্ভাব্য মান।

৩. বিশ্বাসযোগ্যতার স্তর (Confidence Level):

সাধারণত ৯৫% বা ৯৯% ব্যবহার করা হয়।

• ৯৫% বিশ্বাসযোগ্যতার স্তর মানে ৯৫% নিশ্চিত যে প্রাক্কলিত সীমার মধ্যে জনসংখ্যার প্রকৃত মান থাকবে।

৪. ত্রুটি সীমা (Margin of Error):

প্রাক্কলিত সীমার মান নির্ধারণে যে পরিমাণ ত্রুটি থাকতে পারে।

অন্তর প্রাক্কলনের সূত্র

১. জনসংখ্যার গড়ের জন্য অন্তর প্রাক্কলন:

যদি জনসংখ্যার মান বিচ্যুতি (standard deviation) জানা থাকে:
$$\bar{x} \pm Z \cdot \frac{\sigma}{\sqrt{n}}$$

২. নমুনার গড়ের জন্য অন্তর প্রাক্কলন:

যদি মান বিচ্যুতি অজানা থাকে:
$$\bar{x} \pm t \cdot \frac{s}{\sqrt{n}}$$

যেখানে:

• $\bar{x}$: নমুনার গড়
• $Z$: Z-স্কোর (বিশ্বাসযোগ্যতার স্তরের জন্য)
• $t$: t-স্কোর (বিশ্বাসযোগ্যতার স্তরের জন্য)
• $\sigma$: জনসংখ্যার মান বিচ্যুতি
• $s$: নমুনার মান বিচ্যুতি
• $n$: নমুনার সংখ্যা

উদাহরণ

উদাহরণ ১: জনসংখ্যার গড়ের জন্য অন্তর প্রাক্কলন

ধরা যাক, একটি এলাকার নমুনার গড় আয় $৫০,০০০, জনসংখ্যার মান বিচ্যুতি $\sigma = ৫,০০০$, এবং নমুনার আকার $n = ১০০$।
৯৫% বিশ্বাসযোগ্যতার স্তরে, $Z = ১.৯৬$।

$$\bar{x} \pm Z \cdot \frac{\sigma}{\sqrt{n}}$$
$$৫০,০০০ \pm ১.৯৬ \cdot \frac{৫,০০০}{\sqrt{১০০}}$$
$$৫০,০০০ \pm ১.৯৬ \cdot ৫০০ = ৫০,০০০ \pm ৯৮০$$
অতএব, প্রাক্কলিত আয় $৪৯,০২০ থেকে $৫০,৯৮০ এর মধ্যে।

উদাহরণ ২: নমুনার গড়ের জন্য অন্তর প্রাক্কলন

ধরা যাক, নমুনার গড় $২০০, নমুনার মান বিচ্যুতি $s = ২০$, নমুনার আকার $n = ২৫$, এবং ৯৫% বিশ্বাসযোগ্যতার স্তরে $t = ২.০৬৪$।

$$\bar{x} \pm t \cdot \frac{s}{\sqrt{n}}$$
$$২০০ \pm ২.০৬৪ \cdot \frac{২০}{\sqrt{২৫}}$$
$$২০০ \pm ২.০৬৪ \cdot ৪ = ২০০ \pm ৮.২৫৬$$
অতএব, প্রাক্কলিত আয় $১৯১.৭৪৪ থেকে $২০৮.২৫৬ এর মধ্যে।

অন্তর প্রাক্কলনের ব্যবহার

১. অর্থনীতি:

মুদ্রাস্ফীতি, গড় বেতন ইত্যাদির প্রাক্কলন।

২. ব্যবসা:

নতুন পণ্যের চাহিদা নির্ধারণে ব্যবহৃত হয়।

৩. গবেষণা:

পরীক্ষার ফলাফল বিশ্লেষণে ব্যবহার হয়।

৪. স্বাস্থ্য:

রোগীর গড় বয়স বা ওজন প্রাক্কলনে।

সারসংক্ষেপ

অন্তর প্রাক্কলন হলো একটি নির্ভুল এবং কার্যকর পদ্ধতি যা নমুনার তথ্য ব্যবহার করে জনসংখ্যার বৈশিষ্ট্য নির্ধারণ করে। এটি ভবিষ্যৎ সিদ্ধান্ত গ্রহণ এবং পরিসংখ্যান বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে।